“First Law: When a distinguished but elderly scientist states that something is possible, he is almost certainly right. When he states that something is impossible, he is very probably wrong.
Second Law: The only way of discovering the limits of the possible is to venture a little way past them into the impossible.
Third Law: Any sufficiently advanced technology is indistinguishable from magic.”— Arthur C. Clarke
Mass Action Interpretation (M.A.I)
Recall thought-simulation 7 from the previous section. The illustration depicts a collective information retrieval network (I.R.N) for ‘n’ elements, each endowed with a cerebral unit of intelligence (C.U.I) and corresponding stratagems. Based on the concepts discussed thus far, it is evident that the I.R.N plays a vital role in enabling stigmergy, as interpreted graphically in thought-simulation 7 for an aggregation of ‘n’ swarm elements or ‘n’ cogitative elements.
Henceforth, the analysis focuses on an n-element swarm, assuming each element is equipped with a C.U.I and individual stratagems or tactics. The intricacies detailed in Merger-1 and Merger-2 are understood to be intrinsic to the macroscopic elemental interactions modeled using game theory frameworks in this and forthcoming sections.
A large portion (95%) of the game theory models used to represent elemental interactions within the n-element swarm are selected from (Weibull, J.W, 1994). Three distinct conditions are proposed for collective behavioral intelligence, validated in later stages. The analysis is simplified without compromising rigor, but multiple readings may be necessary before fully comprehending the content.
The mathematical models presented are expected to exponentially enhance machine learning paradigms. Reviewing (Weibull, J.W, 1994) beforehand is advisable, either before or concurrently with this and future sections.
NOTE:
- Recall from Merger-1 that stigmergy becomes relevant for brains and nervous systems when assuming they function via indirectly coordinating neuronal elements acting as independent cognitive agencies. Independent I.R.N components can represent brains and nervous systems as complex swarm systems of multiple interacting cognitive agencies, their sets, subsets, and supersets with proportional memory modules. These independent I.R.N components can in turn comprise an interactive I.R.N for an entire brain or nervous system.
- Individual stratagems or tactics will hereafter be referred to as strategies, as the analysis progresses exponentially from this point, alleviating terminology confusion with game-theoretic interpretations of swarm decision-making (including conventional/M.A.I Nash equilibrium, Population Dynamics, and M.M.A.I). This distinguishes stratagems and strategies.
Proposed Conditions for Collective Behavioral Intelligence
Three conditions are proposed as necessary for a system to demonstrate collective behavioral intelligence:
1. The information retrieval network (I.R.N.) dynamically adapts its frame-systems at a frequency f = (1/dt), modulated by the perceived situational dynamics at each instant (dt). This enables the I.R.N. to reflect subtle changes in the collective experience and memory.
2. At each instant (dt), each individual element makes a decentralized choice to address its own locally perceived situation. This suggests pushing decision autonomy to the maximum extent possible within the macroscopic system.
3. Assuming swarm growth rate constancy over a period, individual choices must correspond to Nash equilibria in proportion to swarm growth.
This introduces a solvable optimization problem. The above conditions build on existing research foundations while proposing a formalized approach. Rigorous scientific analysis proves and explores these conditions throughout the remainder of this work across various population dynamics scenarios, assuming reader familiarity with essential game theory (e.g. Weibull, J.W, 1994) or inclination towards analytical proofs.
The following section initiates a game-theoretic interpretation of collective behavioral intelligence, starting with the concept of Nash equilibrium and its meanings.
Beginning a Game-Theoretic Framing of Collective Behavioral Intelligence
This section initiates a game-theoretic interpretation of collective behavioral intelligence. As a reference, the definition of Nash equilibrium is restated: A Nash equilibrium describes the rational strategic choices made by individual logical elements within a system based on the expected actions of other elements.
As stated by Osborne (2004),
“a Nash equilibrium is an action profile a* with the property that no player ‘i’ can improve their outcome by unilaterally changing their action, given that every other player ‘j’ adheres to aj*.”Osborne (2004)
In other words, a Nash equilibrium represents the combination of strategic choices where no one element can gain by singly deviating from the equilibrium point. The following sections explore the implications of Nash equilibria in modeling the emergent collective intelligence within decentralized systems of logical elements and decision-makers. This game-theoretic perspective offers useful formalisms for investigating decentralized collective optimization.
Conventional Interpretation of Nash Equilibrium
The standard conceptualization of Nash equilibrium relies on three core assumptions (Weibull, J.W, 1994):
1. The game is played only once.
2. Players behave rationally to maximize their utilities.
3. The game structure exhibits common knowledge among players.
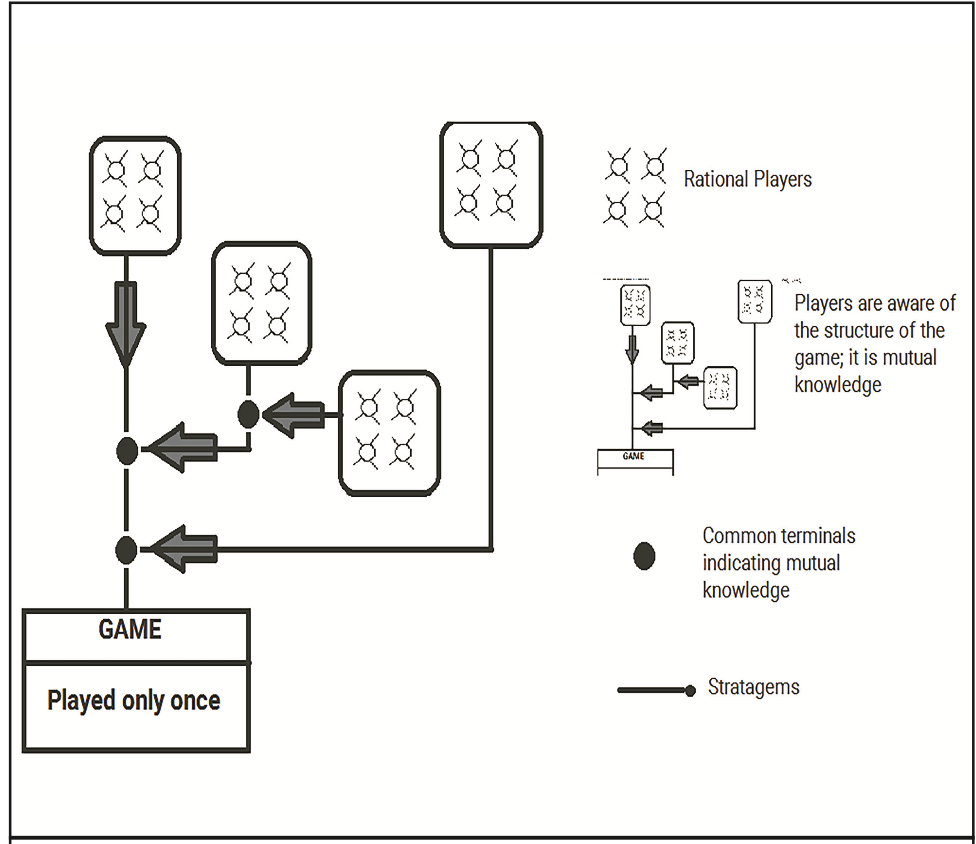
Thought-simulation 8 visually depicts a conventional Nash equilibrium using:
- Four distinct population areas comprising rational cognitive agents (players), with associated strategies.
- Linkages connecting the population areas to a one-shot game.
- Common terminals across players, representing the mutual game structure knowledge.
Mass Action Interpretation (M.A.I) of Nash Equilibrium
The mass-action interpretation of Nash equilibrium makes different assumptions (Weibull, J.W, 1994; Nash, 1950):
1. The game is played repeatedly.
2. Players are not necessarily fully rational.
3. Players need not understand the full game structure.
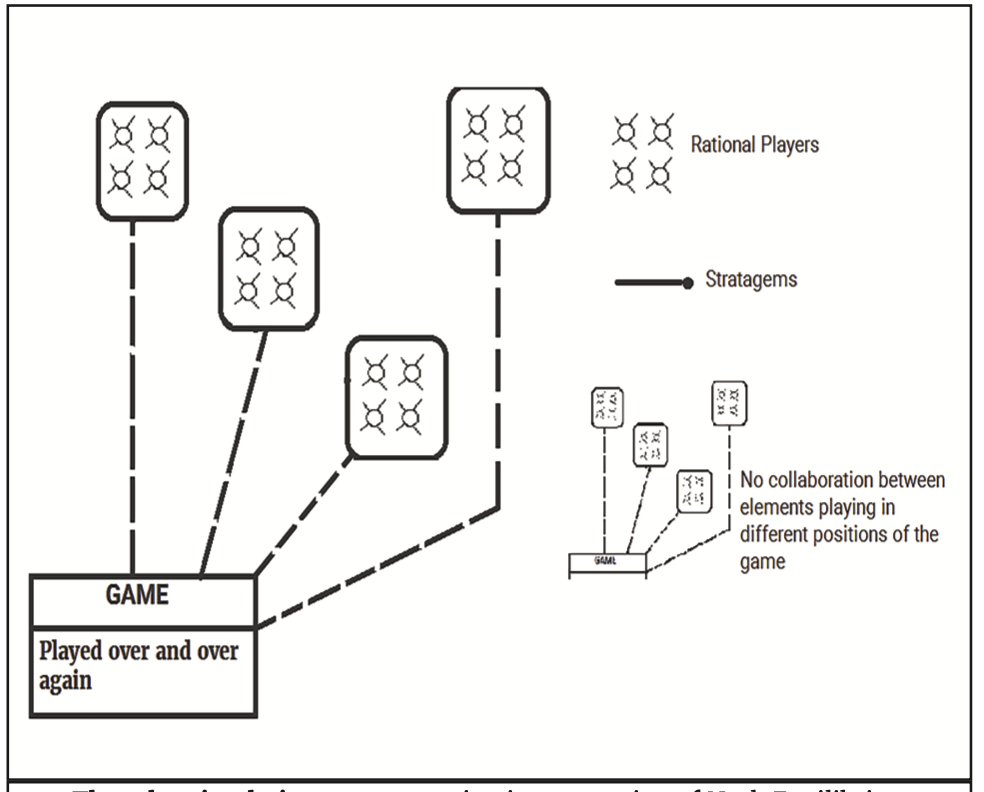
Thought-simulation 9 illustrates these aspects:
- Players are connected to the game with dotted lines, emphasizing their lack of complete structural knowledge.
- Players accumulate empirical data on strategy payoffs through repeated play.
- Participants are distributed across populations.
- Each “average” game iteration randomly samples n participants from the n populations.
- Average strategy usage frequencies stabilize across populations.
To quote,
“To be more detailed, we assume that there is a population (in the sense of statistics) of participants for each position of the game. Let us also assume that the ‘average playing’ of the game involves n participants selected at random from the n populations, and that there is a stable average frequency with which each pure strategy is employed by the ‘average member’ of the appropriate population. Since there is to be no collaboration between individuals playing in different positions of the game, the probability that a particular n-tuple of pure strategies will be employed in a playing of the game should be the product of the probabilities indicating the chance of each of the n pure strategies to be employed in a random playing.”
(Weibull, J.W, 1994) & (Nash, 1950)
NOTE:
- Pure Strategy: A pure strategy constitutes a definitive course of action that a player adopts in every feasible scenario within a game. Pure strategies are deterministic rather than stochastic, unlike mixed strategies which randomize over available actions based on a probability distribution (Jackson, M.O., [2011]).
- Mixed Strategy: A mixed strategy represents a probability distribution that a player utilizes to randomly select between potential actions. Adopting unpredictability allows the player to evade exploitation. In a mixed strategy equilibrium, all players adopt mixed strategies that are optimal responses given the mixing probabilities employed by their opponents (Walker & Wooders, 2008).
Elaborating further on the mass-action conceptualization, we assume a statistical population distribution exists for participants at each strategic position in the game. In an average game iteration, n participants are randomly sampled from these position-specific populations. Over repeated plays, stable average strategy usage frequencies emerge within each population. Since no collaboration occurs between participants in different strategic positions, the probability of observing a particular n-tuple of pure strategies in a given game iteration equals the product of the strategy usage probabilities for each position’s population. In other words, the participant populations independently evolve strategy frequencies, enabling factorization of the joint strategy probability across positions. This core premise allows connecting mass-action equilibrium analysis to aggregate population dynamics – abstracting away from individual rationality to study emergent effects of strategy exploration and payoff-driven diffusion over repeated games.
Now, thought-simulation 10 provides a visual depiction of the following aspect of population dynamics: If si represents the population distribution over the pure strategies α ∈ Ai available to player position i, then the strategy profile s = (si) is formally identical to a mixed strategy profile. Furthermore, the expected payoff to any pure strategy α in a random matching between an n-tuple of individuals, one from each player population, equals the expected payoff πiα(s) when this strategy is played against the mixed strategy profile s.
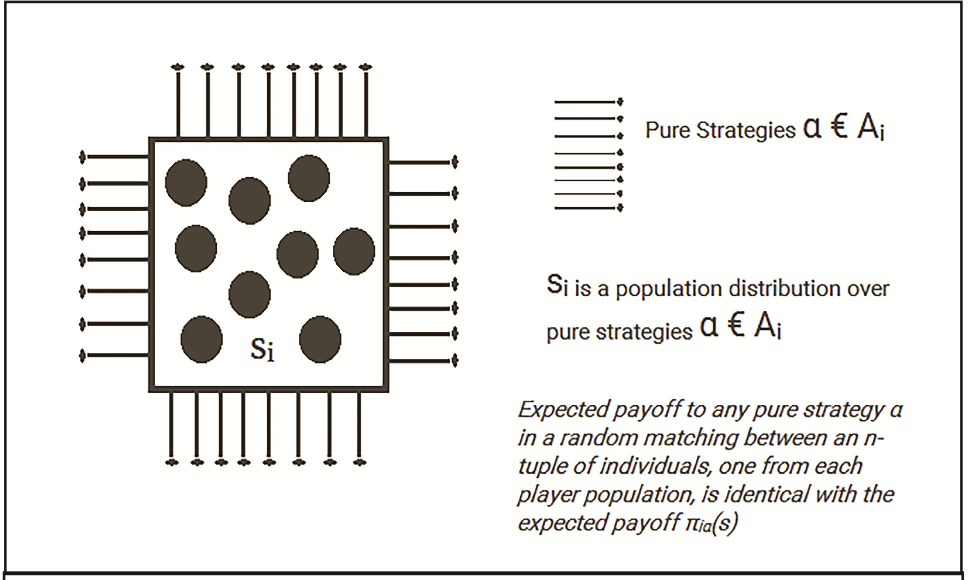
In essence, the pure strategies α are distributed across the population si for adoption, forming the mixed strategy profile s. Thus, the expected payoff to α against s is the same as its expected payoff in strategic play between individuals randomly sampled from the populations, as illustrated in thought-simulation 10. Moreover, if over time the players “accumulate empirical information on the relative advantages of the various pure strategies available to them” (Weibull, J.W, 1994), then:
- The players in position i know the payoffs πiα(s).
- Knowing πiα(s), they will use only the “optimal pure strategies” (see equation 9).
- Since si represents the strategy profile in its domain, positive coefficients are ascribed to the “optimal pure strategies”, satisfying the condition for s to be an equilibrium point.
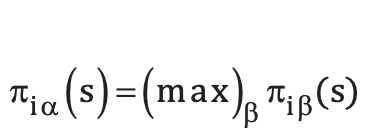
A mathematical correlation with swarms can be made based on the established allocations, as illustrated in thought-simulation 11 (see below). The image shows a set of player positions (for brevity, only four positions are depicted). In this analysis, each player position corresponds to a set of elements in the swarm, each equipped with pure strategies in its domain, denoted as before. A game dG represents a strategic interaction constrained by rules. Every such interaction must eventually lead to some consequence that generates appropriate payoffs for all participating elements (possible if the elements cooperate in a self-enforcing or non-cooperative way). In summary, thought-simulation 11 illustrates a game dG with player positions mapping to swarm elements adopting pure strategies. The strategic interactions between swarm elements are governed by rules and yield payoffs reflecting the consequences of self-enforced or non-cooperative behavior. This establishes a mathematical correlation between the game allocations and swarm dynamics.
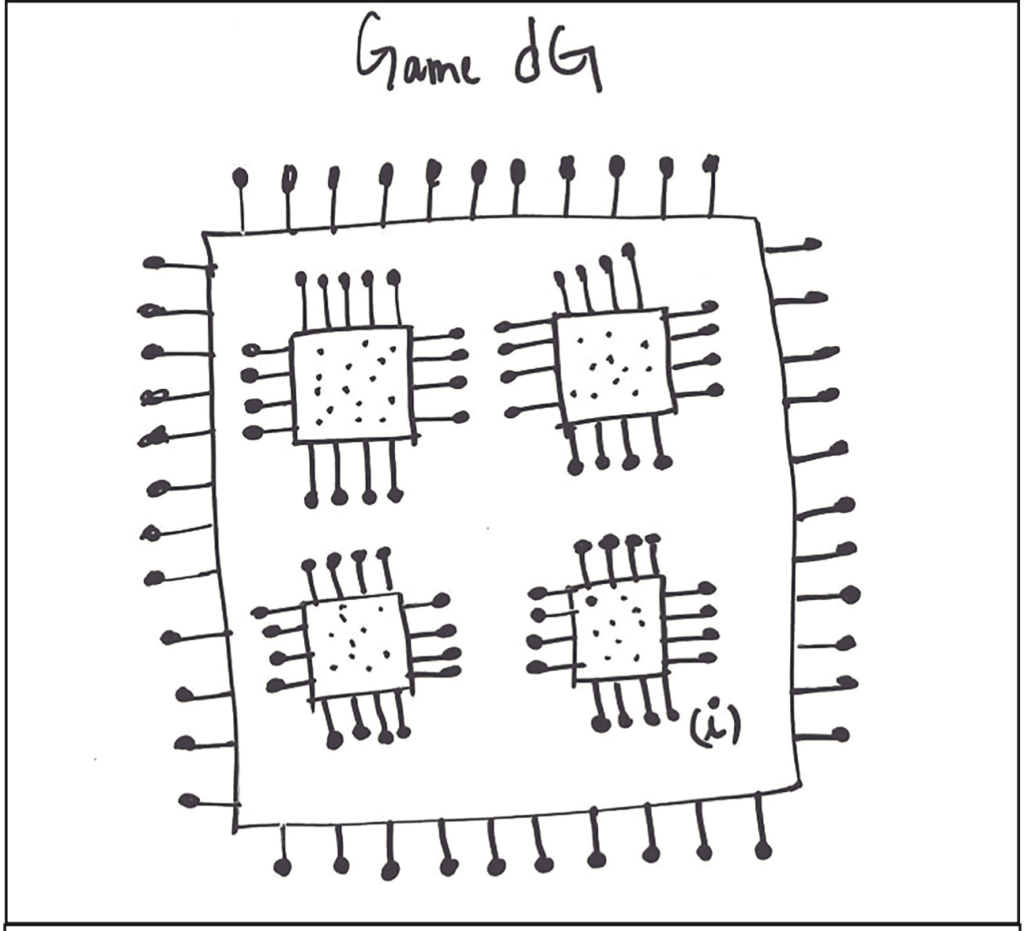
In this case, the swarm elements are players of the game dG, which represents a strategic interaction. Sets of pure strategies are distributed across player positions, forming their corresponding mixed strategy profiles. Each player position is assumed to have its own pure strategy set that it applies perfectly in the interaction, meaning each position with its population of swarm elements emulates a single player. Thus, the case can be assessed more concisely if needed by reconsidering dG as a finite game between n elements.
“A strategy profile s is called interior (or completely mixed) if all pure strategies are used with positive probability.” (Weibull, J.W, 1994)
Game dG consists of all pure strategies across all positions, represented as distributed over dG’s global domain. In thought-simulation 11, all pure strategies are redrawn over the entire game to denote their spread, forming a polyhedron of mixed strategy profiles.
Now, for a player position i (thought-simulation 11) if siα is the probability assigned to α ∈ Ai, the strategy profile s ∈ S will be a Nash equilibrium iff siα>0 implies πiα(s) = maxβ∈Aiπiβ(s) as in Equation 9. Numbers πiα(s) represent a mixed strategy equilibrium point, with the following properties:
“the mixed strategies representing the average behavior in each of the populations form an equilibrium point” (Weibull, J.W, 1994).
“… some sort of an approximate equilibrium, since the information, its utilization, and the stability of the average frequencies will be imperfect” (Weibull, J.W, 1994).

In the above strategic setting, the finite game dG is played a number of times (finite) by n players occupying element positions {1,…,n}. Strategies are distributed across dG in two forms: Ai is the pure strategy set for player i, S is the mixed strategy set, and S is the polyhedron of mixed strategy profiles. πiα(s) denotes the expected payoff to player i when using pure strategy α ∈ Ai against s ∈ S. And πi(s) is the expected payoff to player i under the profile s=(s1,…,sn) ∈ S. Thus, the game is defined as dG = (I, S, π).
If over time the players “accumulate empirical information on the relative advantages of the various pure strategies available to them” (Weibull 1994), this implies the “optimal pure strategies” πi(s) = maxβ∈Ai πiβ(s) are assigned positive probabilities by the population distribution Si (a population distribution over pure strategies α ∈ Ai).
An amplified version of the interaction is presented next for ‘n’ player positions. In alignment with the M.A.I framework, the game dG should be played repeatedly by elements randomly sampled from infinite populations, with each population occupying a player position in every iteration of dG. This repetitive playing of the game by randomly drawn elements from infinite populations is depicted visually in thought-simulation 12.
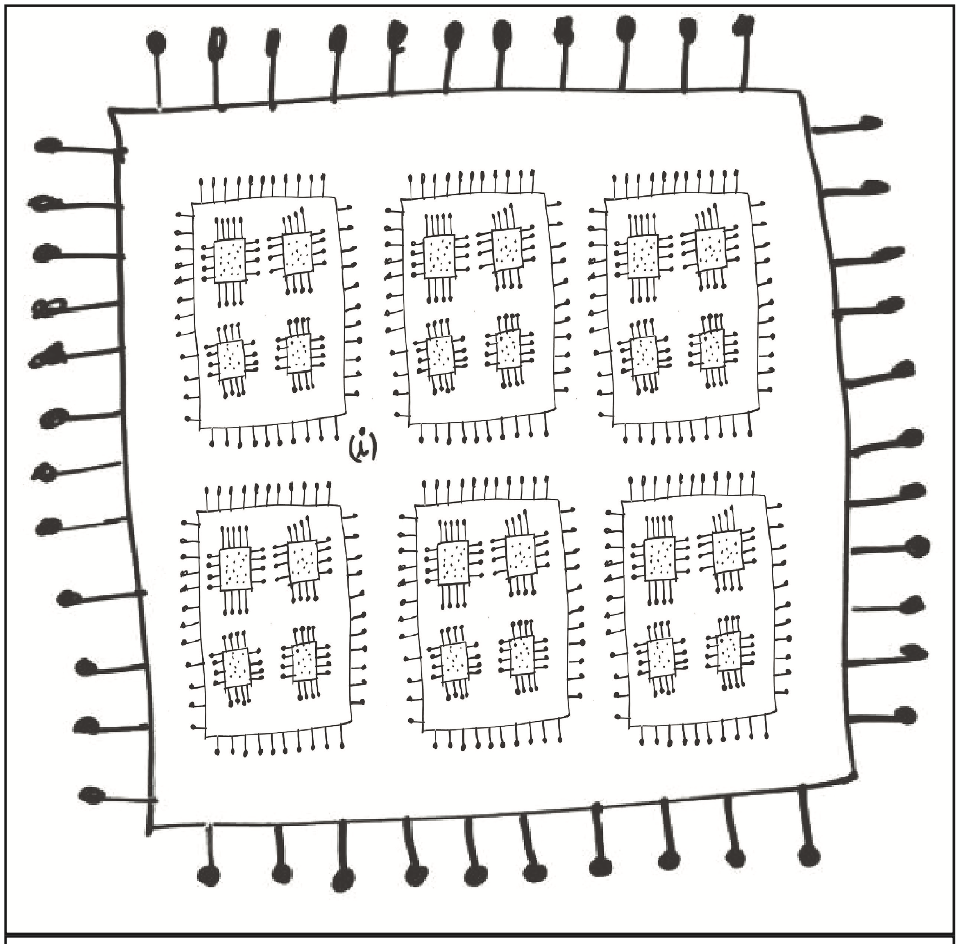
In the mega-game N.dG, the game dG is played N times by players randomly drawn from infinite populations. Each population in N.dG maps to a player position i. Every mixed strategy profile subset s ∈ S in N.dG represents a population state, where si ∈ Si denotes the distribution of pure strategies in position i. Specifically, siα is the probability that a randomly drawn element from population i uses pure strategy α ∈ Ai in N.dG. Consequently, πiα(s) is the expected payoff to an element in population i playing pure strategy α, and πi(s) is the average expected payoff across population i. Therefore, the mega-game is defined as N.dG = N.{(I,S,π)}, playing dG N times with infinite population sampling.
“A pure strategy a ∈ A will be said to be extinct in population state if its population share siα is zero. A state in which no pure strategy is extinct is called interior.” (Weibull, J.W, 1994)

An insightful conclusion can be drawn from the formulated M.A.I framework:
“Suppose that every now and then (say, according to a statistically independent Poisson process) each individual reviews her strategy choice. By the law of large numbers, the aggregate process of strategy adaptation may then be approximated by deterministic flows, and these may be described in terms of ordinary differential equations.” (Weibull, J.W, 1994)
The analysis in this section clearly demonstrates the importance of Nash equilibria in modeling the dynamics of large, strategically interacting populations represented as swarms. As summarized by Weibull, J.W (1994),
“…Nash equilibria could be identified as stationary, or perhaps dynamically stable, population states in dynamic models of boundedly rational strategy adaptation in large strategically interacting populations.”
The game N.dG presented in this section provides the basis for investigating various cases of population dynamics discussed in Weibull, J.W. (1994). The next blogpost will examine specific cases that identify stable Nash equilibrium states for different population state descriptions. These cases are studied under the assumption that the aggregate process of strategy adaptation can be approximated by deterministic flows and modeled using ordinary differential equations. By expanding the current understanding of N.dG into these population dynamics examples, the next blogpost (merger-4) aims to estimate and elucidate the mass action interpretation of Nash equilibrium.
Furthermore, the analytical analysis conducted here clearly demonstrates that Nash equilibrium states play a critical role in populations of cognitive entities, specifically large, strategically interacting populations represented as swarms. As stated by Weibull, J.W. (1994), “Nash equilibria could be identified as stationary, or perhaps dynamically stable, population states in dynamic models of boundedly rational strategy adaptation in large strategically interacting populations.”
The research article by Nowak and Sigmund (2004) summarizes the significance of evolutionary game theory for enabling a computational and mathematical approach to analyzing biological adaptation and coevolution. As they discuss, this game theoretic framework is more suitable than optimization algorithms for studying frequency-dependent selection. The replicator and adaptive dynamics models describe short- and long-term evolution in phenotype space and have been applied broadly across areas ranging from animal behavior to human language. To quote,
“Darwinian Dynamics based on mutation and selection form the core of mathematical models for adaptation and coevolution of biological populations. The evolutionary outcome is often not a fitness maximizing equilibrium but can include oscillations and chaos. For studying frequency-dependent selection, game theoretic arguments are more appropriate than optimization algorithms. Replicator and adaptive dynamics describe short- and long-term evolution in phenotype space and have found applications ranging from animal behavior and ecology to speciation, macroevolution, and human language. Evolutionary game theory is an essential component of a mathematical and computational approach to biology.” (Nowak, M.A & Sigmund K, 2004)
For a more comprehensive understanding of the population dynamics cases covered in the upcoming blogs, the reader may refer to Nowak and Sigmund (2004) and Weibull, J.W. (1994).
References
[1] Weibull, J.W. (1994). The Mass-Action Interpretation of Nash Equilibrium. Industriens Utredningsinstitut – The Industrial Institute for Economic and Social Research, 427, 1-17.
[2] Osborne, M.J. (2004). An Introduction to Game Theory.
[3] Nash, J. (1950). Non-Cooperative Games. Mathematics Department, Princeton University. Princeton University.
[4] Jackson, M.O. (2011). A Brief Introduction to the Basics of Game Theory. 1-21. Retrieved from https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1968579
[5] Walker, M., Wooders, J. (2008). Mixed Strategy Equilibrium. In: The New Palgrave Dictionary of Economics. Palgrave Macmillan, London.
[6] Nowak, M.A & Sigmund K. (2004). Evolutionary Dynamics of Biological Games. SCIENCE, 303, 793-798.